Gang Min

꾸준히 기록하는 블로그.

Playing Atari with Deep Reinforcement Learning

Playing Atari with Deep Reinforcement Learning

Abstract

  • Fist deep learning model using reinforcement learning
    • Successfully learn control policies directly
    • From high-dimensional sensory input
  • CNN model trained on a variant of Q-learning
    • Input : raw pixel, output: a value function estimating future reward
  • Applied seven Atari 2600 games (no adjustment)
    • Outperforms ALL previous approaches on six games
    • Surpasses a human expert on three games

Problem to solve : motivation

  • Learning directly from high dimensional sensory input

  • Most successful RL relies on hand-crafted features

  • 많은 사람들이 high dimensional sensory를 direct로 받고 싶었으나 이루어지지 않고 있었음. 대부분의 강화학습은 사람들이 만들어낸 feature로 진행하고 확장성이 떨어지는 단점이 있다.

Remaining challenges: cannot directly apply DL to RL

  • Most DL requires hand labeled training data
    • RL must learn from a scalar reward signal
    • Reward signal is often sparse, noisy, and delayed
    • delay between actions and resulting rewards can be thousand time steps
  • Most DL assumes data samples are independent
    • RL encounters sequences of highly correlated states

Solutions

  • CNN with a variant Q-learning
  • Experience replay

Agent and Environment

  • RL에서는 a라는 action을 취하면 action의 결과로 reward r이 돌아오고 동시에 상태인 o를 볼 수 있다.
  • 경험은 액션을 취함으로써 돌아오는 것들의 sequence $o_1,r_1,a_1,…,a_{t-1},o_t,r_t$
  • 경험을 모은것을 state라고 한다. $s_t = f(o_1,r_1,a_1, …,a_{t-1},o_t,r_t)$

Major Components of an RL Agent

  • An RL agent may include one or more of these components:
    • Policy: agent’s behavior function
      • 어떤 상태에 있을 때 뭘 해야되는지 알려준다.
        • Deterministic policy : $a = \pi(s) 항상 일정한 정책 즉 똑같은 액션이 돌아온다 $
        • Stochastic policy : $\pi(a \mid s) = P[a \mid s] $확률로 돌아온다.
    • Value function: how good is each state and/or action
      • state s에서 어떤 행동을 하면 보상을 얼마나 받을 것인지.
        • Q-Value는 어떤 행동을 했을 때 기대되는 보상
        • $Q^\pi(s,a) = E[r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3}+ … \mid s, a] $
        • Q를 배우는 과정은 Bellman equation으로 나타낼 수 있다.
          • $Q^\pi (s,a) = E_{s’,a’} [r+ \gamma Q^\pi (s’,a’) \mid s, a] $
            • 바로 받은 reward랑 그 다음 상태로 갔을 때 Q function에서 가장 큰 값을 더하면 된다.
        • 풀어서 봤을 때는 $Q^\ast(s,a) = \underset{\pi}\max Q^\pi(s,a) = Q^{\pi^\ast} (s,a) $
          • 상태와 액션을 줬을 때 가장 optimal한 Q function을 optimal이라고 하고 *을 붙여준다.
          • optimal은 Q가 가질 수 있는 최대값을 가져온다는 뜻.
    • Model: agent’s representation of the environment

value based RL

  • Q-networks
    • Represent value function by Q-network with weights w
    • $Q(s, a, w) \approx Q^* (s, a) $
    • w를 가지고 있는 Q가 optimal한 Q를 닮아가도록 만드는게 목표
  • Q-learning
    • Optimal Q-values should obey Bellman equation
      • $Q^*(s,a)= E_{s’} [r + \gamma \underset{a’}\max Q(s’,a’)^\ast \mid s,a] $
    • Treat right -hand side $r + \gamma \underset{a’}\max Q(s’,a’,w) $
    • Minimize MSE loss by stochastic gradient descent
      • $I = (r + \gamma \underset{a’}\max Q(s’,a’,w) - Q(s,a,w))^2 $
        • $ y를 r+ \gamma \underset{a’}\max Q(s’,a’,w), \hat{y}은 Q(s,a,w)로 해서 LOSS function을 구한다 $
        • r은 진짜값 Q(s,a,w)는 랜덤한 값

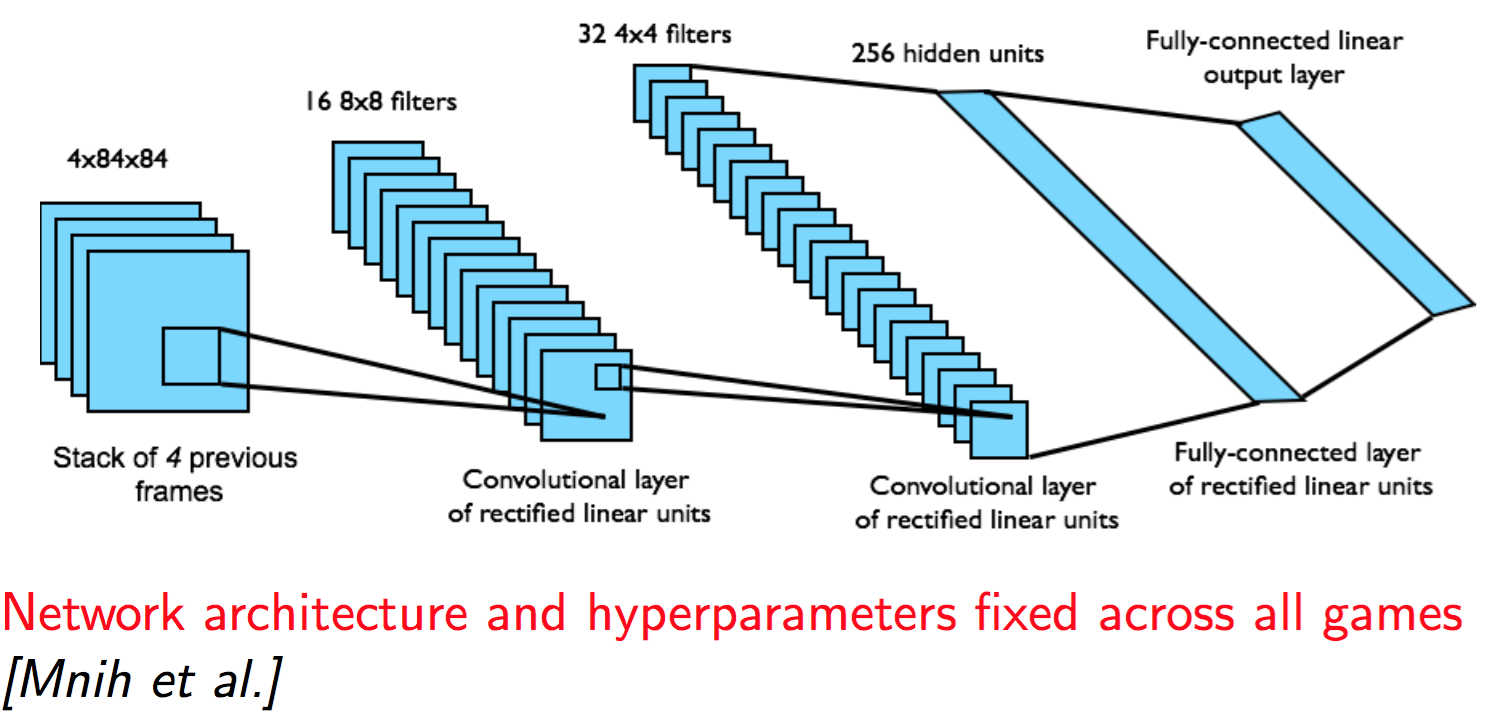
DQN in Atari

  • End-to-end learning of values Q(s,a) from pixels s
  • input state s is stack of raw pixels from last 4 frames
  • Output is Q(s,a) for 18 joystick/button positions
  • Reward is change in score for that step
  • 최근에 나오는 네트워크에 비해서 깊지는 않다
  • partially observable state 화면 하나만 보여주면 왼쪽으로 움직이는지 오른쪽으로 움직이는지 알 수 없는 것을 방지하기 위해서 화면을 4개를 동시에 사용. 액션은 화면 네번에 한번.
  • state를 x(sequence)라고 생각하면 된다 화면 4개

Training and Stability

  • Q는 안정적으로 converges되는 것을 보여줌.

References

Comments

You May Also Enjoy